LE PLAISIR DE CHERCHER
(Recherche réalisée avec la classe CM2a de Rians)
Pierre Eysseric
I.U.F.M. Centre de Draguignan
IREM de Nice
e.mail: mathsenstockpeysseric@minitel.net
Dans cet article, rédigé à la suite de l'atelier animé au cours des journées APMEP de Marseille, nous présenterons d'abord brièvement le dispositif expérimenté depuis 6 ans dans quelques classes des écoles primaires du Var: la mise en place d'un lieu et d'un temps pour le plaisir de chercher en mathématiques; puis nous illustrerons celui-ci par la chronique d'une recherche réalisée dans une classe de CM2 au cours de l'année scolaire 97/98; enfin nous renvoyons le lecteur intéressé par de plus amples informations sur notre travail à la bibliographie annexée.
1 Présentation du dispositif.
Il s'agit de transposer dans les classes de l'école primaire un style de travail, celui des chercheurs en mathématiques. L'image de cercles concentriques centrés sur l'enfant (ou sur le chercheur) permet une description assez simple de cette transposition.
1.1 De la recherche à la publication.
Le premier cercle est constitué par l'enfant et son sujet de recherche, c'est à dire une question qu'il se pose, qui rentre dans le champ des mathématiques et à laquelle il a envie de pouvoir répondre; le sujet peut être proposé par l'enfant ou par un tiers (l'enseignant par exemple) mais dans tous les cas l'élève doit se l'être approprié et se sentir responsable de la recherche d'une solution au problème posé.
Le deuxième cercle comprend deux ou trois élèves: ceux qui ont le même sujet de recherche ou des copains avec lesquels on parle librement de son travail; son équivalent dans la communauté scientifique, ce sont les collègues du laboratoire, ceux que l'on accroche au détour d'un couloir ou devant la machine à café pour leur faire part d'une idée, d'une question, d'un obstacle rencontré, d'un article intéressant, ... Ce cercle, bien que très informel, n'est pas sans importance; c'est un espace de liberté: on peut travailler seul mais on a aussi le droit d'échanger avec d'autres, de parler sans contraintes de son travail; cela a une incidence non négligeable sur l'implication des enfants dans l'activité de recherche et la découverte du plaisir de chercher.
Le troisième cercle, c'est la classe (les élèves et leur enseignant) qui fonctionne ici un peu comme un laboratoire avec son directeur de recherche. Après un temps de recherche plus au moins long les enfants vont devoir présenter leur travail à toute la classe; on peut arriver avec des solutions à proposer mais aussi avec des questions restées sans réponse, sur lesquelles on ne parvient plus à avancer. Dans ce cas on explique ce que l'on a essayé, les impasses dans lesquelles on s'est retrouvé et chacun peut intervenir pour proposer de nouvelles pistes ou pour critiquer ce qui a été fait. A l'issue de ce débat deux situations peuvent se présenter: soit on estime que les idées échangées permettent de se remettre au travail sur ce sujet, soit on aboutit à un constat collectif d'impasse et on décide de se documenter ou de renvoyer la question au quatrième cercle (un référent mathématique extérieur à la classe qui peut être un chercheur ou un professeur de mathématiques). Lorsque par contre, l'enfant estime avoir résolu le problème qu'il s'était posé, ses solutions sont soumises à la critique sans pitié des autres élèves et de l'enseignant si cela est nécessaire; il s'agit donc de convaincre toute la classe de la valeur des réponses proposées. Si le travail présenté est accepté, validé par la classe, il va pouvoir sortir de celle-ci, être publié; cette publication pourra prendre des formes diverses: affichage dans le couloir, article dans le journal de l'école, fax adressé à une autre classe pratiquant la recherche en mathématiques, courrier envoyé à un chercheur correspondant de la classe, ... On entre alors dans le quatrième cercle, mais avant d'en arriver là plusieurs allers et retours entre le premier et le troisième cercle sont souvent nécessaires et il n'est pas rare qu'un enfant arrivé convaincu d'avoir une excellente réponse doive à l'issue d'une discussion parfois acharnée convenir qu'il doit se remettre à l'ouvrage. Dans ce troisième cercle le rôle de l'enseignant comme directeur de recherche est fondamental: c'est lui qui régule les échanges, qui gère les allers et retours entre recherche et communication jusqu'à la validation d'un résultat à publier ou au constat qu'on ne sait pas et au recours à une aide extérieure.
Le quatrième cercle est extérieur à la classe: à l'origine du projet, c'était un chercheur, un spécialiste des mathématiques auquel on peut envoyer les travaux de la classe (des résultats, mais aussi des questions restées sans réponse), quelqu'un d'extérieur à la classe, à l'école et qui peut être le garant de la qualité mathématique des travaux réalisés et ainsi autoriser leur publication. En fait, dans la pratique, les choses se sont souvent passées différemment, ce quatrième cercle se traduisant surtout par la publication , la communication hors la classe des travaux de recherche des enfants.
Enfin le dernier cercle est le congrès annuel des enfants chercheurs: tous les ans, les enfants qui ont fait au cours de l'année scolaire des travaux de recherche en mathématiques viennent les présenter au cours du congrès Maths en Stock. Lors des premiers congrès, les effectifs étant peu nombreux, la présentation prenait la forme de communications orales. Avec entre 300 et 450 participants aux derniers congrès Maths en Stock, nous avons privilégié la communication par voie d'affiche et l'organisation d'ateliers de recherche en mathématiques. Ce congrès est un peu l'aboutissement du travail de toute une année tout en étant aussi pour certains enfants un tremplin vers d'autres recherches à travers les sujets découverts au cours de la journée. C'est une sorte de fête des mathématiques et l'engouement des enfants surprend souvent les parents accompagnateurs. " Ils sont fous; c'est leur sortie de fin d'année, on leur fait faire des maths toute la journée, et en plus, ils sont contents! ", nous a dits l'un d'eux.
1.2 Un lieu et un temps pour le plaisir de chercher en mathématiques.
Après cette description des différentes étapes de la recherche en classe, revenons sur quelques mots clefs qui permettent de mieux comprendre les activités proposées.
"Un lieu".
Les recherches en mathématiques se déroulent dans la classe, avec l'enseignant de celle-ci. Il ne saurait être question pour nous de transférer cette activité en dehors de la classe et de faire une sorte de club mathématique, ou de la confier à un intervenant extérieur. Les ateliers de recherche en mathématiques (que nous désignerons par ARM dans la suite du texte) doivent faire partie du travail de la classe et ne pas se situer à côté. Dans la mesure où nous espérons un impact des ARM sur les apprentissages en mathématiques des enfants, leur immersion dans les activités ordinaires de la classe nous semble fondamentale. Nous voulons éviter de produire un dédoublement des mathématiques dans la tête des enfants: d'un côté, les "maths sympa" du club math ou de l'intervenant extérieur, et de l'autre les "maths rasoir" de la classe, du maître ou de la maîtresse. L'unité de lieu est une condition nécessaire au maintien de l'unité des mathématiques.
"Un temps".
Les ARM sont un des moments de l'activité mathématiques des enfants dans la classe; un moment important, mais un moment limité: selon les classes, les ARM représentent en moyenne entre 30 min et 1 h par semaine. L'ARM, lieu d'apprentissage d'une démarche, doit avec et non remplacer l'apprentissage des savoirs figurant au programme de mathématiques de la classe. L'objectif à terme est de faire évoluer l'image que les enfants ont des mathématiques et de leur permettre d'aborder dans un autre état d'esprit les apprentissages plus classiques.
"Le plaisir".
Nous voulons faire découvrir aux enfants des mathématiques qui peuvent être source de plaisir au même titre que la lecture, la musique, la peinture, ... Cette découverte passe par la liberté: peut-il y avoir plaisir si on fait des mathématiques parce qu'on y est contraint? Et la question peut légitimement être posée du caractère obligatoire ou facultatif de cette activité. Nous avons choisi de proposer les ARM à tous les enfants pour deux raisons. D'une part, un enfant ne peut découvrir qu'il est possible de chercher en mathématiques et d'y trouver du plaisir, si on ne lui en offre pas l'opportunité; d'autre part, cela nous semblait indispensable pour ne pas isoler les ARM des autres apprentissages. Mais par ailleurs nous ouvrons malgré avec les ARM un espace de liberté dans la classe du fait que nous nous affranchissons pour un temps de la contrainte des programmes, et que l'enfant a le libre choix des problèmes qu'il va chercher à résoudre: il n'est confronté qu'à des questions qui ont stimulé sa curiosité et qu'il se pose réellement.
"Chercher en mathématiques".
Après l'évocation de l'espace de liberté des ARM, voici deux mots qui fixent le cadre, l'objet du travail. Tout est possible; la seule contrainte est de chercher et de le faire dans le champ des mathématiques. Mais tous les acteurs de l'ARM (élèves, enseignant, chercheur) ne mettent pas les mêmes réalités derrière ces mots et tout au long de l'année, le contenu des ARM va être l'objet d'une négociation dans la classe. " Est-ce bien de la recherche? Sont-ce des mathématiques? " Ces deux questions reviendront sans cesse dans la bouche de l'enseignant comme dans celles des enfants. Par un processus analogue à celui fonctionnant chez les personnages mis en scène par Imre Lakatos dans Preuves et réfutations au sujet des polyèdres convexes, les enfants vont, tout en pratiquant la recherche en mathématiques, faire évoluer leur définition de celle-ci. Cette négociation permanente est un élément fondamental pour comprendre l'impact des ARM sur l'ensemble des apprentissages à l'école (les élèves manifestent dès le démarrage d'un ARM leurs conceptions à la fois des mathématiques et de la recherche, et c'est la pratique de la recherche en mathématiques qui va les conduire progressivement à réviser celles-ci) et l'investissement des enfants dans ce type d'activité (beaucoup d'enfants se remettent à exister en tant que sujet face aux mathématiques, ce dont ils ne soupçonnaient plus la possibilité.
2. Chronique d'une recherche:
Cette chronique a été rédigée à partir d'une part de la correspondance entre la classe du CM2 de l'école de Rians et M. Yves Lafont, chargé de recherches au CNRS (IML de Luminy), et de l'enregistrement audio du travail réalisé par les enfants lors de la visite du chercheur dans leur classe. Pour la retranscription des dialogues quelques abréviations seront utilisées: C désignera le chercheur, M le maître de la classe et Ei un élève.
2.1 Travail en Atelier de Recherche en Mathématiques:
* construction d'une dizaine de solides (le matériel utilisé est le matériel Polydron: faces polygonales en plastique rigide s'emboîtant les unes dans les autres).
* observation des solides; comptage des faces, des arêtes et des sommets; organisation des résultats dans un tableau.
* formulation d'un premier problème:
"Les faces, c'est assez facile à compter; mais pour les arêtes ou les sommets, c'est plus dur! Est-il possible de trouver un moyen de calculer le nombre d'arêtes ou de sommets sans les compter?"
* ce problème amène les enfants à rechercher une éventuelle relation entre le nombre de faces, le nombre d'arêtes et le nombre de sommets d'un même solide.
2.2 Formulation devant la classe des résultats obtenus:
* plusieurs enfants ont redécouvert à partir des résultats consignés dans leur tableau la loi d'Euler:
Nombre de faces + Nombre de sommets - 2 = Nombre d'arêtes
* cette loi est exposée à la classe, discutée et vérifiée sur les différents solides fabriqués.
* toute la classe s'étant mise d'accord sur la formulation de la loi, un courrier pour Yves Lafont est préparé.
* l'enfant qui tape le fax se trompe: il inverse arêtes et sommets; ainsi le document que recevra le chercheur (fax du 27/11/97) contiendra des résultats erronés, ce qui n'était pas le cas au moment de l'exposition en classe...En outre deux questions sont posées au chercheur:
Est-ce que cette règle est générale pour tous les solides?
Peut-on trouver une loi qui nous donne le nombre d'arêtes et de sommets en connaissant le nombre de faces?
2.3 Réponse par fax du chercheur:
" Bonjour la classe " Les Pies "
J'ai bien reçu votre fax, et j'aimerais en savoir un peu plus sur vous. Par exemple, en quelle année êtes-vous? Combien êtes- vous? Quel est le nom de votre professeur?
Votre recherche porte sur un domaine très intéressant des mathématiques, qui s'appelle la topologie. Je pense que vous avez fait une confusion, sans doute entre les sommets et les arêtes. Pouvez-vous m'envoyer les dessins (ou les patrons) des solides que vous avez construits?
Cela dit, il y a une formule qui vaut pour beaucoup de solides, mais pas pour tous. Essayez donc de construire un solide qui ressemble à une bouée, c'est-à-dire avec un trou au milieu (les mathématiciens appellent cela un tore).
Essayez aussi de construire deux solides (sans trous) qui ont le même nombre de faces, mais pas le même nombre de sommets. Cela peut répondre à votre deuxième question."
2.4 Arrivée du chercheur dans l'école:
* celle-ci coïncide avec la réception du texte ci-dessus par les enfants; on retourne au travail en ARM pour:
- corriger la loi si elle est erronée;
- représenter les solides fabriqués pour illustrer la loi obtenue.
2.5 Travail en ARM en présence du chercheur:
* à partir des solides, tableau et loi sont rectifiés.
* plusieurs enfants se lancent dans la représentation des solides par un de leurs patrons; cela débouche sur de nouvelles découvertes:
- des solides différents peuvent avoir le même nombre de faces avec des nombres d'arêtes et de sommets qui diffèrent;
- Sébastien propose un chercheur une méthode pour compter les arêtes et les sommets d'un solide sur son patron.
2.6 Exposition, formulations des découvertes du matin:
* écriture de la loi corrigée:
Nombre d'arêtes = Nombre de faces + Nombre de sommets - 2
* vérification collective de la loi sur les différents solides (de nouveaux solides ont été fabriqués au cours de l'ARM du matin).
* retour aux deux questions que les enfants avaient posées au chercheur:
- à propos de la première, il leur rappelle la suggestion faite dans sa réponse écrite: essayer de construire un solide qui ressemble à une bouée.
- mais la discussion s'engage rapidement sur la deuxième question: peut-on trouver une loi qui nous donne le nombre d'arêtes et de sommets en connaissant le nombre de faces?
Marlène et Michaël répondent "non" en présentant les deux solides à 8 faces qu'ils ont fabriqués:
le solide de Marlène (prisme à base hexagonale)
8 faces 12 sommets 18 arêtes
le solide de Michaël (octaèdre régulier)
8 faces 6 sommets 12 arêtes
Ils recomptent, vérifient la loi devant la classe et disent:
"Non, on ne peut pas car 8 faces donnent 6 et 12, ou 12 et 18 pour les sommets et les arêtes."
Un autre élève prend alors la parole:
"Moi je dirais non, car on est obligé d'avoir les faces et les sommets, ou les faces et les arêtes. Si on a les faces et les sommets, on peut calculer les arêtes:
Nombre d'arêtes = Nombre de faces + Nombre de sommets - 2
Si on a les faces et les arêtes, on peut calculer les sommets:
Nombre de sommets = Nombre d'arêtes + 2 - Nombre de faces."
* l'enfant écrit les deux formules au tableau; il s'ensuit une discussion autour de différentes formules proposées par les enfants:
Nombre de sommets = Nombre d'arêtes - Nombre de faces + 2
"C'est la même chose dans un ordre différent:"
"Les deux formules, c'est pareil: dans la première, on ajoute 2 aux arêtes et ensuite on enlève les faces; dans la deuxième, on enlève d'abord les faces, puis on ajoute 2, c'est pareil!"
La formule: Nombre de faces = Nombre d'arêtes - Nombre de sommets + 2 , est proposée pour calculer les faces.
"Les faces, ça ne sert à rien de les calculer; c'est facile à compter!"
* les enfants prennent visiblement plaisir à ce nouveau jeu "trouver de nouvelles formules", mais il faut signaler que la plupart des formules sont énoncées en s'appuyant sur les nombres d'une ligne du tableau (un solide particulier):
"8 (faces) = 12 (arêtes) -6 (sommets) + 2"
puis sont vérifiées sur les autres solides.
* le chercheur leur propose une formule qu'aucun élève n'a énoncée jusqu'ici:
peut-on écrire Nombre de sommets = 2 - Nombre de faces + Nombre d'arêtes ?
E: "oui, on a juste changé l'ordre; mais pour calculer, il faudrait aller dans les "moins"."
2.7 La bouée de Vivien:
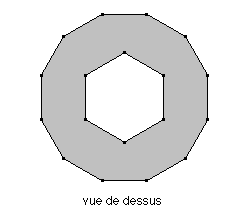
* pendant la discussion ci-dessus, Vivien a construit un solide en forme de bouée; il vient le présenter et on organise le comptage des faces, des arêtes et des sommets.
C'est un prisme droit à faces latérales carrées (12 extérieures et 6 intérieures) et de base ci-dessous:

* à propos des arêtes non saillantes "du trou de la bouée", surgit alors une question:
E1: "Est-ce que ça, c'est une arête?"
E2: "Oui, c'est une arête, car là, on compte une face, et une autre face à côté."
C: "On peut décider qu'une arête, c'est toujours la limite entre deux faces; comme cela, on ne se trompera pas; d'habitude les arêtes sont un peu comme une montagne; là on a des arêtes "presque plates" ou comme des vallées."
* un enfant remarque que le "dessus" et le "dessous" sont identiques et que cela peut raccourcir le comptage.
* Le comptage aboutit à: 42 faces 78 arêtes 36 sommets
On calcule alors: Nombre de faces + Nombre de sommets - 2
et on trouve ... 76.
La formule serait-elle fausse pour la bouée de Vivien?
E1: "Il y a une erreur dans le nombre de sommets; on en a compté deux de moins."
M: "Et si c'était le nombre d'arêtes qui soit faux!"
C: "Ou une erreur pour les faces..."
E2: "Non, les faces, on sait les compter; c'est facile sans se tromper!"
E3: "Il y a une erreur de 2, ou alors la loi ne marche pas."
C: "Et pourquoi la loi ne marcherait pas avec ce solide?"
E3: "Il doit y avoir une autre loi."
C: "Une autre loi pour quels solides?"
E3: "A partir d'un nombre limité d'arêtes, de sommets, de faces, on change de loi."
C: "Quand il y a beaucoup de faces, de sommets ou d'arêtes?"
E4: "A partir d'un certain nombre de faces, il faut changer la loi!"
On note la proposition au tableau:
Quand le nombre de faces devient grand, on change de loi.
C: "Ce serait intéressant de fabriquer d'autres solides avec beaucoup de faces, de sommets, d'arêtes; avec au moins 42 faces... Il serait aussi intéressant de fabriquer une autre bouée."
2.8 Retour à la recherche individuelle (ou en petits groupes):
* On vérifie le comptage pour la bouée de Vivien.
* On fabrique d'autres solides pour savoir si la loi change, et quand est-ce qu'elle change.
* Certains utilisent ce temps pour s'approprier les lois qui ont été écrites au tableau au cours de la discussion en les vérifiant sur des solides.
2.9 Le solide de Sébastien:
* L'annonce de la fabrication d'un nouveau "gros" solide interrompt le travail et ramène la classe à la discussion collective.
"Voilà le nouveau solide que j'ai fait; bon là, il y a des trous, mais c'est des faces..." (il a manqué de pièces et il raisonne sur un solide en partie construit avec des pièces en plastique et en partie "pensé").
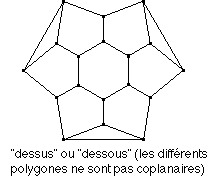
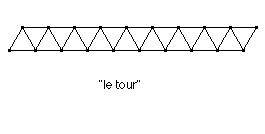
* le comptage aboutit à: 38 faces 36 sommets 72 arêtes
et on vérifie que la loi marche...
E: "Peut-être que la loi change entre 38 et 42..."
On en restera là pour l'instant: la recherche est à poursuivre...
2.10 Discussion autour du comptage des faces du solide de Sébastien:
E1: "Il n'y a que 19 faces, car "tout ça" (en montrant la partie supérieure du solide), c'est une seule face."
* on recompte avec cette "convention" et on aboutit à 20 faces.
E2: "Je ne comprends pas pourquoi ça (le tour), tu dis que c'est plusieurs faces; si c'était rond (allusion à un cylindre), là, cela ne compterait qu'une seule face."
C: "Est-ce que cela change le nombre d'arêtes?"
E2: "Il compte les arêtes par petits morceaux et il dit que le haut, c'est une seule face!... Pour moi, il y a 3 faces, 2 arêtes ... et pas de sommets!"
* La discussion est très animée sur ce qu'est une arête ou une face pour de tels "gros" solides; on touche là à des questions de nature topologique...(équivalence entre prisme et cylindre). La question ne sera pas tranchée et sera renvoyée à une éventuelle recherche ultérieure.
"Nous avons du mal à définir les faces dans le cas des bouées." (fax du 14/3/98)
2.11 Le comptage des sommets et des arêtes sur un patron:
Sébastien présente ce qu'il a trouvé le matin:
* la pyramide à base triangulaire (tétraèdre): "4 faces: des triangles réguliers."
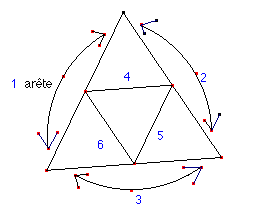
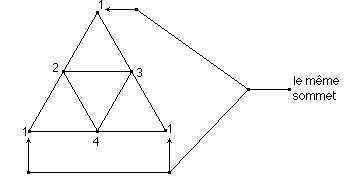
"Quand on referme "ça" et "ça", ça va se toucher! ... donc 4 arêtes."
"Tout ça là, c'est un seul sommet, donc 4 sommets."
Critique: "Et pour un grand patron?"
Réponse: "C'est pareil! ça marche pour toutes les pyramides..."
* Et il recommence avec la pyramide à base carrée:
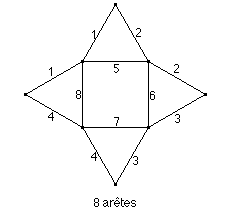
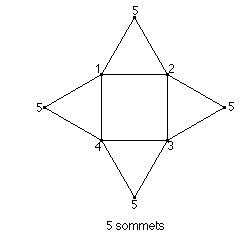
* Il ne parvient pas à retrouver l'extension de sa méthode qu'il avait proposée le matin pour le prisme à base triangulaire. Voici ce qu'il avait expliqué au chercheur:
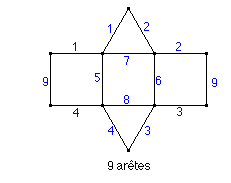
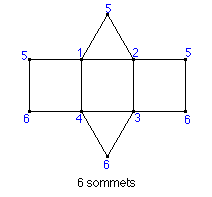
* Il propose alors d'essayer sa méthode pour le cube; après quelques hésitations, il y parvient pour les sommets:
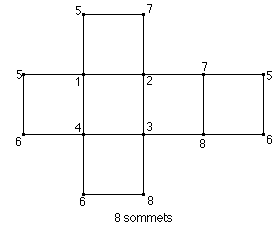
"5 "' et "6" sont identifiés moins rapidement que les autres:
"Quand on rabat, ça va se coller là-haut et ça fait le même sommet."
Pour les arêtes, un coloriage des regroupements 2 par 2 des segments du bord du patron lui permet de conclure avec l'aide du chercheur...
2.12 Conclusion de la journée:
* On renvoie au prochain ARM les questions en suspens et la mise au propre des formulations.
* Mais les enfants voudraient poursuivre et plusieurs, avant de sortir, annonce qu'ils ont de nouveaux solides à tester.
* On repart avec:
- une loi reliant faces, arêtes et sommets, qui marche pour tous les solides fabriqués, sauf pour la bouée de Vivien; si cette loi change lorsque le nombre de faces est grand, c'est entre 38 et 42.
- une méthode pour compter les arêtes et les sommets sur le patron qui fonctionne bien pour les pyramides, mais n'est pas encore tout à fait au point pour les autres solides.
3 Bibliographie:
Arsac G. & al [1991]: Problème ouvert et situation-problème. Irem de Lyon.
Assude T. & al [1995]:La question de la "transposition du sens". Actes de SFIDA 4, IMa-CNR,Genova, IV p. 15 à 20.
Assude T. [1996]: Styles de travail: relations entre l'éducation mathématique et l'épistémologie, in Actes de l'Université d'été européenne, histoire et épistémologie dans l'éducation mathématique, vol. II, p. 389 à 395.
Assude T. [1997]: L'atelier de recherche mathématique: problèmes de temps et de mémoire, Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.
Audin P. et Duchet P. [1989]: La recherche mathématique à l'école: "Math en Jeans", Séminaire de didactique des disciplines scientifiques, LSD2-IMAG, Grenoble.
Audin P. et Duchet P. [1989]: 1000 classes, 1000 chercheurs: 1 millième, APMEP, Paris.
Bachelard G. [1938]: La formation de l'esprit scientifique, PUF, Paris.
Baruk S. [1985]: L'âge du capitaine (de l'erreur en mathématiques), Seuil, Paris.
Bassis H. [1984]: Je cherche donc j'apprends, GFEN, Messidor, éditions sociales.
Bkouche R., Charlot B. & Rouche N. [1991]: Faire des mathématiques: le plaisir du sens, Armand Colin, Paris.
Boulanger P. [1984]: La fête des petits matheux, Tomes 1 et 2, Belin, Paris.
Brousseau G. [1986]: Fondements et méthodes de la didactique des mathématiques, RDM, Vol. 7-2, p. 83 à 115, La Pensée Sauvage, Grenoble.
Charnay R. [1992]: Problèmes ouverts, problèmes pour chercher, Grand N, n° 51, p. 77 à 83.
Chevallard Y. [1985]: La transposition didactique, La Pensée Sauvage, Grenoble.
Cohen G. & al [1995]: Récré-Maths, Editions Pôle, Paris.
Dossier: "Culture mathématique et enseignement" [1991], Cahiers pédagogiques n° 299.
Eysseric P. & al [1993]: Le plaisir de chercher, document vidéo, IUFM de Nice, Service audiovisuel du centre de Draguignan.
Eysseric P.[1994]: Le plaisir de chercher, journal de liaison entre les ARM, n°1 (oct.-nov. 94), IUFM de Nice, centre de Draguignan.
Eysseric P. & al [1996]: Le plaisir de chercher, in Le plaisir de chercher et autres textes ..., IUFM de Nice.
Eysseric P.[1998]: Le plaisir de chercher, atelier B2, in Actes du XXIVième Colloque Inter-Irem des formateurs et professeurs chargés de la formation des maîtres, St Etienne, mai 1997.
Floridi C. [1996]: Pour une pratique des problèmes ouverts: un exemple en classe de CE1/CE2, Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.
GERME [1988]: Modalités pour une pratique autonome des mathématiques, IRDP, Neuchâtel.
Groupe "Jeux et Maths" [1982, 1985 et 1990]: Jeux 1, 2 et 3, Brochures APMEP n° 44, n° 55 et n° 78, APMEP, Paris.
Groupe "Jeux et Maths" [1995]: Fichier Evariste, Brochure APMEP n° 98, APMEP, Paris.
Lakatos I. [1976]: Preuves et réfutations, Hermann, 1984, Paris.
Lang S. [1984]: Serge Lang fait des maths en public, Belin, Paris.
Lang S. [1984]: Serge Lang, des jeunes et des maths, Belin, Paris.
Legrand M. [1989]: Rationalité et démonstration mathématiques, le rapport à une communauté scientifique, RDM, Vol. 9-3, p. 365 à 406, La Pensée Sauvage, Grenoble.
Legrand M. [1993]: Débat scientifique en cours de mathématiques, Repères Irem n° 10, Topiques éditions.
Legrand P. & al [ 1988]: Table ronde sur la curiosité en mathématiques, bulletin vert APMEP, P. 151 à 170, Paris.
Lohou-Delvoye [1995]: Le contrat didactique dans l'apprentissage de la résolution de problèmes, Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.
Margolinas C. [1993]: De l'importance du vrai et du faux dans la classe de mathématiques, La Pensée Sauvage, Grenoble.
Marill F. [1996]: La communication dans la recherche mathématique à l'école, , Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.
Monteils V. [1995]: Le plaisir de chercher, , Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.
Nimier J. [1976]: Mathématique et affectivité, Stock, Paris.
Nimier J. [1985]: Les maths, le français, les langues ... à quoi ça sert?, Cedic Nathan, Paris.
Petroff G. [1995]: Recherches en mathématiques d'enfants du cycle 3: essai d'élaboration d'un document cadre pour la mise en place de cette activité dans les classes, , Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.
Polya G. [1962]: Comment poser et résoudre un problème?, Editions. J. Gabay 1989, Paris.
Reboa P. [1995]: La recherche en mathématiques au cycle 3 et la démarche scientifique, , Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.
Sensevy G. [1996]: Le temps didactique et la durée de l'élève. Etude d'un cas au cours moyen: le journal des fractions, RDM, Vol. 16-1, p. 7 à 46, La Pensée Sauvage, Grenoble.
Van der Meer R. & Gardner B. [1994]: MATHS, Seuil, Paris.
Zagdoun-Dantzer S. [1996]: Comment surmonter les obstacles que pose la mise en place d'activités de recherche mathématique au cycle 3?, Mémoire professionnel PE2, IUFM de Nice, Centre de Draguignan.